条件概率：三硬币问题

坑边闲话：以前我的社长，每次跟我讨论概率问题时，都特别强调，“我们所有的概率观测，实际上都是条件概率”。之前我不太懂这句话是什么，但是今天推导“三硬币问题”的时候，我发现用条件概率模型更加简单。

• 知乎原文

三硬币模型：假设有 3 个硬币，标号为 $A$，$B$，$C$. 三枚硬币都是不均匀的，抛掷得到正面的概率分别为 $\pi$、$p$、$q$. 现在进行这样一个实验：先抛掷硬币 $A$，如果得到正面，就抛掷硬币 $B$，否则就抛掷 $C$. 抛掷 $B$ 或者 $C$ 的结果，为本实验的结果。注意，中间抛掷 $A$ 的结果，我们不关心，而且也看不到. 现在问，如果你只知道重复若干次本实验的结果，不能观看实验过程，你能否恢复出参数 $\pi$、$p$、$q$？

再次提醒：你只能看到连续多次实验的结果，对于 $\pi$、$p$、$q$ 一无所知。现在要求你根据观测结果，恢复 $\pi$、$p$、$q$.

现在猜测一下，如果结果中频繁出现正面，那么说明硬币 $B$ 和 $C$ 中至少有一个侧重出现正面，如果两个都偏向出现正面，那么硬币 $A$ 的正面概率将不太好预测；还有一种可能，硬币 $B$ 和 $C$ 的正面概率不等，一个高一个低，不妨设 $B$ 更容易出现正面，$C$ 更容易出现反面，那么 $A$ 应该倾向于让结果由 $B$ 决定，即 $A$ 更容易出现正面。

1. 解题思路·

为了方便建立公式，我们令 $\theta =(\pi ,p,q)$，$\theta$ 也就是我们要得到的目标。

另设随机变量 $y$ 是观测结果，表示一次三硬币实验的观测结果，取值在 $S=0,1$. 该变量我们是可以观测到的。

另外，中间的硬币 $A$ 的结果，我们看不到，于是假设其值为随机变量 $z$，因为这个变量无法观测，我们称之为“隐形的变量”，简称隐变量。

再次强调，随机变量 $y$ 是可观测的，随机变量 $z$ 是不可观测的。

那么根据全概率公式，我们有：

$$ \mathbb{P}{\theta}(y) = \sum_z{\mathbb{P}{\theta}(y,\ z)} $$

提醒：这种形式可能在国内教科书上不常见，但是更加合理，不要再用 “$|$” 来划分观测变量和已知情况了。

现在我们的目标是把上式中的 $z$ 消掉，否则含有隐变量的式子没什么意义。

对于条件概率下的联合概率，只需要把它们看作一个整体就可以，所以再次根据条件下的联合概率公式，就有

$$ \begin{aligned} \mathbb{P}{\theta}(y) &= \sum_z{\mathbb{P}{\theta}(y,\ z)} \ &= \sum_z{\mathbb{P}{\theta}(z)\cdot \mathbb{P}{\theta,\ z}(y)} \end{aligned} $$

上述概率其实非常简单，根据样本空间理论，可以画个 Venn 图：

图 1：在概率意义下，最外围的绿色图形的面积为 1，其余的小矩形的面积自然都是小数值，也就是概率的意义。中间部分的阴影部分，占据条件事件 $z$ 的面积的比例，就是条件概率。

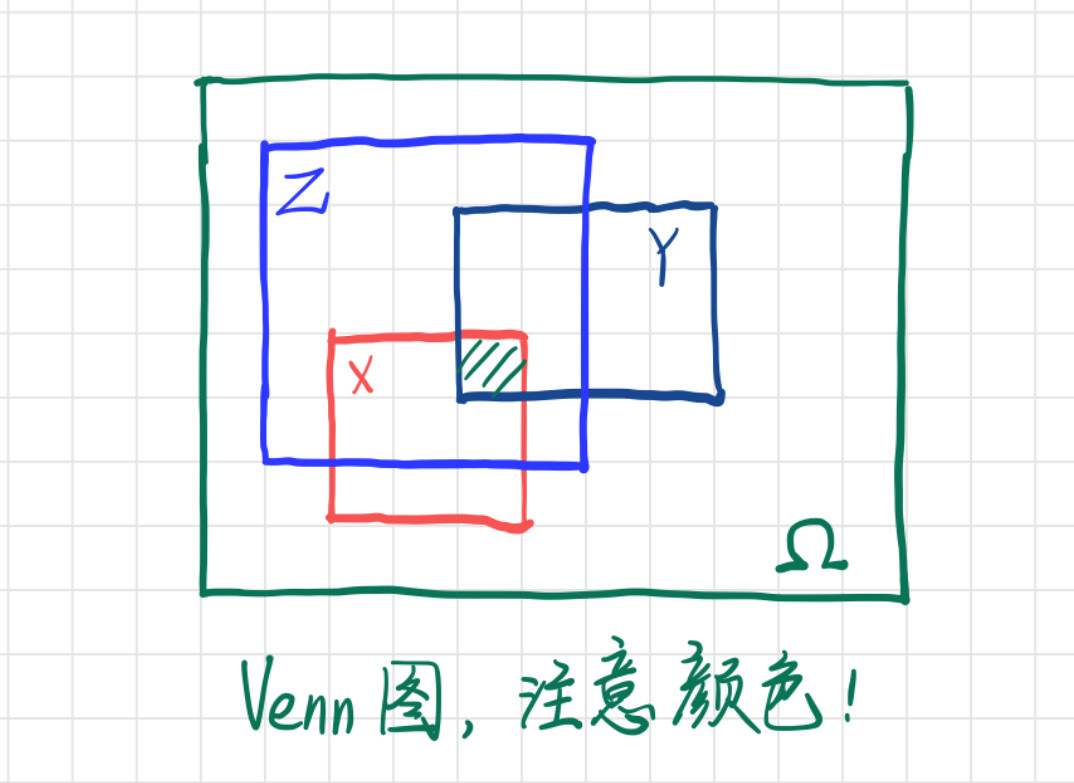
通过图 1，我们可推导一下：

图 2：该图中的颜色要与图 1 完全对应起来看。最后一行公式即一般数学书上的表示形式。

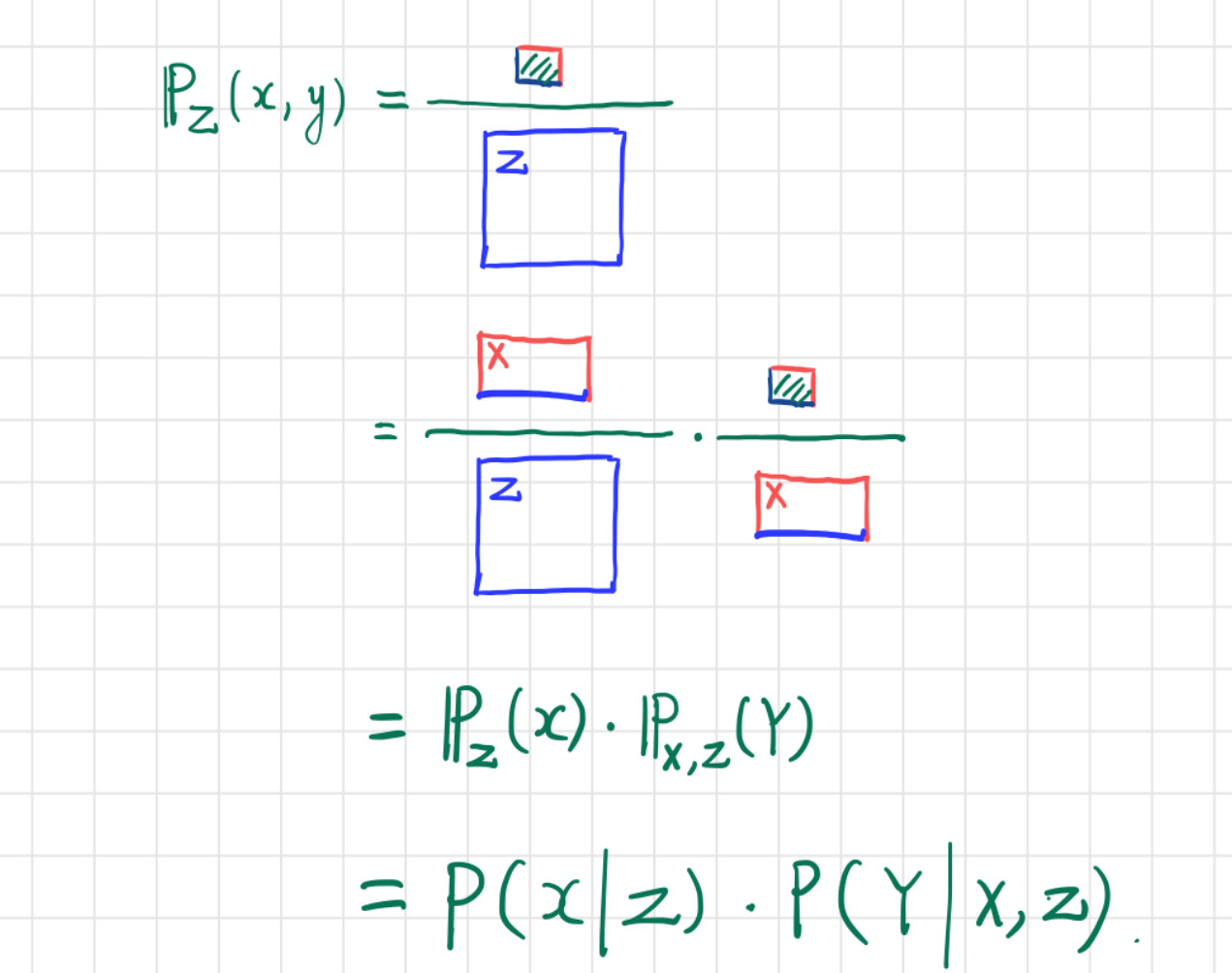
通过 $\theta =(\pi ,p,q)$ 的意义，我们反代入，得到

$$ \begin{aligned} \mathbb{P}{\theta}(y) &= \sum_z{\mathbb{P}{\theta}(y,\ z)} \ &= \sum_z{\mathbb{P}{\theta}(z)\cdot \mathbb{P}{\theta,\ z}(y)}\ &= \pi p^y(1-p){1-y} + (1-\pi)q^y(1-q){1-y} \end{aligned} $$

公式解释：$z$ 有两种结果：当 $z$ 朝上，$\mathbb{P}{\theta}(z)$\mathrm{取}\mathrm{值}\mathrm{为}$\pi$，\mathrm{即}$A$\mathrm{硬}\mathrm{币}\mathrm{朝}\mathrm{上}\mathrm{时}，$y$\mathrm{的}\mathrm{结}\mathrm{果}\mathrm{取}\mathrm{决}\mathrm{于}\mathrm{硬}\mathrm{币}$B$，$\mathbb{P}{\theta,\ z}(y)$\mathrm{与}$p$\mathrm{相}\mathrm{关}；\mathrm{反}\mathrm{之}，$y$\mathrm{的}\mathrm{结}\mathrm{果}\mathrm{取}\mathrm{决}\mathrm{于}\mathrm{硬}\mathrm{币}$C$，$\mathbb{P}_{\theta,\ z}(y)$\mathrm{与}$q$\mathrm{相}\mathrm{关}。\mathrm{上}\mathrm{标}\mathrm{的}$y$ 只是为了方便描述两种情形而已。

自此我们就成功地将观测结果与 $\theta =(\pi ,p,q)$ 联系起来了。虽然这么做，不如直接根据概率路径选择做简单。

考虑重复这个实验很多次，得到了一列观测结果 $Y=(y_1,y_2,\cdots ,y_n)$，同时假设相应的隐变量取值为 $Z=(z_1,z_2,\cdots ,z_n)$. 那么观测数据的似然函数为

$$ \mathbb{P}{\theta}(Y) = \sum{Z}\mathbb{P}{\theta}(Z)\mathbb{P}{\theta,\ Z}(Y) $$

坑边闲话：其实写成上述矩阵、向量的形式没什么意义，只是看着好看而已。

写成一般形式，就是：

$$ \mathbb{P}{\theta}(Y) = \prod{j=1}^{n}\pi p^{y_j}(1-p){1-y_j} + (1-\pi)q^{y_j}(1-q){1-y_j} $$

一串独立同分布的随机变量，出现一串值，自然是每个单独取值概率的乘积。

这时候调用 EM　算法，求模型参数　$\theta =(\pi ,p,q)$ 的极大似然估计即可。

$$\hat{\theta }=\arg max\log ({\mathbb{P}}_{\theta }(Y))$$

总结·

三硬币模型是一个很有趣的问题，描述背后的原理不难，用极大似然估计求出参数才是有技术含量的。接下来我将利用最大期望方法求解该问题。

Cover 劳动节第三篇文章